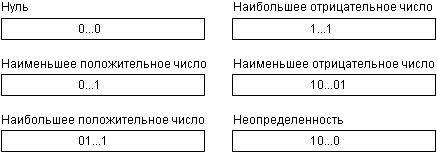
Аппаратное обеспечение персонального компьютера

Целые числа

Арифметический сопроцессор наряду с вещественными числами способен обрабатывать и целые числа. Он имеет команды, выполняющие преобразования целых чисел в вещественные и обратно.

Возможно четыре формата целых чисел:

·          целое число;

·          короткое целое число;

·          длинное целое число;

·          упакованное десятичное число

Целое число занимает два байта. Его формат полностью соответствует используемому центральным процессором. Для представления отрицательных чисел используется дополнительный код. Короткое целое и длинное целое имеют аналогичные форматы, но занимают, соответственно, 4 и 8 байт.

Упакованное десятичное число занимает 10 байт. Это число содержит 18 десятичных цифр, расположенных по две в каждом байте. Знак упакованного десятичного числа находится в старшем бите самого левого байта. Остальные биты старшего байта должны быть равны 0.

Существуют команды сопроцессора, которые преобразуют числа в формат упакованных десятичных чисел из внутреннего представления в расширенном вещественном формате. Если программа делает попытку преобразования в упакованный формат денормализованных чисел, нечисел, бесконечности и тому подобных, в результате получается неопределенность. Неопределенность в упакованном формате представляет из себя число, в котором два старших байта содержат единицы во всех разрядах. Содержимое остальных восьми байтов произвольно. При попытке использовать такое упакованное число в операциях фиксируется ошибка.

Мы подробно рассмотрели формат представления вещественных чисел и отметили, что в этом формате для представления отрицательных чисел используется специальный знаковый бит. Для целых чисел используется дополнительный код.

В дополнительном коде положительные числа содержат нуль в самом старшем бите числа:

0XXX XXXX XXXX XXXX

Для получения отрицательного числа в дополнительном коде из положительного надо инвертировать каждый бит числа и затем прибавить к числу единицу.

Например, число +5 в дополнительном коде выглядит следующим образом:

0000 0000 0000 0101 = +5

Для получения числа -5 вначале инвертируем значение каждого бита:

1111 1111 1111 1010

Теперь прибавим к полученному числу +1:

1111 1111 1111 1011 = -5

На рис. 10.3 мы привели все возможные варианты представления целых чисел.

Рис. 10.3. Возможные представления целых чисел

Формат упакованного десятичного числа показан на рис. 10.4.

Рис. 10.4. Формат упакованного десятичного числа

На этом рисунке n0...n17 означают разряды десятичного числа. Они могут изменяться в пределах от 0000 до 1001, то есть от 0 до 9 в десятичной системе счисления.

Теперь, после того как мы рассмотрели форматы данных, с которыми может работать арифметический сопроцессор, можно перейти к изучению внутренних регистров сопроцессора.